Der folgende Text ist nach dem Urhebergesetzt geschützt. Reproduktion oder Nutzung dieses Textes durch konventionelle, elektronische oder beliebige andere Verfahren ist nur im nicht-kommerziellen Rahmen gestattet. Verwendungen in größerem Umfang bitte zur Information bei DANTE e.V. melden. Für kommerzielle Nutzung ist die Zustimmung des Autors einzuholen.

Kopien dieses Textes für eigene Internet-Seiten sind nicht gestattet. Es ist jedoch gestattet einen Link auf diese Seite auf eigenen Internet-Seiten zu verwenden.

Inhalt

Einleitung
oder „Warum ist ein Satzspiegel eigentlich wichtig?“

Der Satzspiegel ist wie der Rahmen eines Bildes. Ein echter Rembrandt in einem schiefen, bunten, neonfarbenen PVC-Rahmen wird immer wie eine billige Kopie wirken. Ebenso wird ein inhaltlich perfektes Dokument mit verkorkstem Satzspiegel nicht die Geltung erfahren, die es verdient. Obwohl diese Tatsache unstrittig sein sollte, wagen sich Laien immer wieder daran, eigene Satzspiegel zu entwerfen. In einigen Fällen werden dabei Einstellungen aus Textverarbeitungsprogrammen übernommen, die kaum die Bezeichnung „Satzspiegel“ verdienen, geschweige denn als Konstruktion zu bezeichnen sind.

Bei einigen Laien haben sich auch Schlagworte und Teile der damit verbundenen Konstruktionen festgesetzt. Leider sind den Ergebnissen, die dieses Halbwissen zeitigt, oft die nicht beachteten Voraussetzungen der Satzspiegelkonstruktion deutlich anzusehen. Aber auch wenn sie anderen Laien nicht auf den ersten Blick unangenehm auffallen, so können sie unterschwellig einen unerwünschten Eindruck erzeugen. Deshalb folgen nun zunächst einige grundsätzliche Überlegungen zu Satzspiegeln.

Allen Satzspiegeln gemeinsam
oder „Welche Rolle spielt Harmonie in der Satzspiegelkonstruktion?“

Jan Tschichold war unbestreitbar eine der schillerndsten Persönlichkeiten in der Typografie des 20. Jahrhunderts. Dies liegt sicher darin begründet, dass seine typografischen Aufsätze und Abhandlungen eine Sprache verwenden, die man eher in einem Roman als in einem wissenschaftlichen Werk vermuten würde. Einige behaupten, Tschichold sei der Begründer der modernen Typografie. Andere sehen in ihm im Gegenteil einen überholten Verfechter konservativen Denkens. Das Eigenartige am Typografen Tschichold ist, dass er sich anscheinend häufig widerspricht. In Wahrheit jedoch lassen seine Aufsätze bei zeitlicher Einordnung einen lernenden und wachsenden Geist erkennen. Die scheinbaren Widersprüche sind dabei keine sich wandelnden Grundsätze, sondern Neubewertungen an Hand fester Grundsätze.

Diese Grundsätze haben auch in der modernen Typografie ihre Berechtigung, wenn sie auch für den Profi kein zwingendes Korsett darstellen. Für den Laien jedoch haben diese Grundsätze den unschätzbaren Vorteil, dass sie ihm das Leben erleichtern. Wenn die Grundsätze eingehalten sind, ist die Wahrscheinlichkeit, dass das Ergebnis negativ bewertet werden muss, gering. Je mehr die Grundsätze verletzt sind, desto dünner wird das Eis. Während also der Profi weiß, was er tut, und Verletzungen der Grundsätze bewusst einsetzen kann, sollte der Laie sie meiden wie der Teufel das Weihwasser.

Der wichtigste Grundsatz in der Typografie, von dem viele anderen Regeln abgeleitet werden, lautet: Harmonie! Das menschliche Auge oder besser gesagt, die Sinne des Menschen streben ständig in gleicher Weise nach Harmonie wie das Universum nach Chaos strebt. Was Harmonie im Einzelnen bedeutet, ist auch Bestandteil der Kultur. Da es hier um Typografie des Westens geht, bestimmt die westliche Kultur den zugrunde liegenden Harmoniebegriff.

Es stellt sich damit die Frage, wann eine Seite harmonisch ist. Um diese Frage beantworten zu können, müssen zunächst die bestimmenden Größen einer Seite festgestellt werden. Der ungeübte Laie wird sagen: die Breite beziehungsweise Höhe der Ränder oder des Satzspiegels. Genaugenommen hat er damit nicht unrecht. Leider bieten aber die absoluten Größen wenig Möglichkeit einer schematischen Betrachtung. So lässt sich eine Frage, ob ein äußerer Rand von 2 cm besser ist als ein äußerer Rand von 3 cm, kaum beantworten, wenn man nicht weiß in welcher Beziehung oder welchem Verhältnis dieser Rand zu anderen Elementen der Seite steht. Schon allein, um eine Satzspiegelkonstruktion nicht allein für eine Papiergröße anwenden zu können, sind deshalb die Verhältnisse der Elemente und innerhalb der Elemente einer Seite die bestimmenden Größen.

Wir alle kennen aus dem Alltag Verhältnisse, die uns besonders harmonisch erscheinen. So gilt das Seitenverhältnis eines Fernsehgeräts oder Computermonitors mit 4 : 3 oder eines Breitformatbildes mit 16 : 9 als harmonisch. Auch andere Verhältnisse mit besonderen Eigenschaften gelten als sehr harmonisch. Der goldene Schnitt spielt dabei eine wichtige Rolle. Der goldene Schnitt ist die Lösung des folgenden Problems: Wie muss ein Ganzes geteilt werden, so dass zwei ungleiche Teile entstehen, bei denen das Verhältnis des kleineren Teils zum größeren Teil dem Verhältnis des größeren Teils zum Ganzen entspricht? Tabelle 1 gibt zu einem gegebenen kleinen Teil a jeweils das errechnete größere Teil b und das Ganze c an.

In der Typografie werden jedoch in der Regel die ganzzahligen Verhältnisse verwendet, die in Tabelle 2 angegeben sind. Besonders interessant ist hier die fortlaufende Reihe 1 : 2 : 3 : 5 : 8 : 13 : 21 : 34 : 55 : 89..., die erstaunlich genau ist. Wir werden darauf noch zurückkommen. Diese Reihe entspricht übrigens der Fibonacci-Reihe, bei der man ein Glied aus der Summe der beiden Vorgänger erhält. Dies ist eine zusätzliche Harmoniebeziehung.

Ein anderes bekanntes, ganzzahliges Verhältnis ist der Villardsche Teilungskanon. Bei diesem wird ein Ganzes so in zwei Teile zerlegt, dass das kleinere Teil halb so groß ist wie das Größere. Es beschreibt also das Verhältnis 1 : 2. Dieses passt auch zum ganzzahligen goldenen Schnitt.

Neben besonderen Verhältnissen spielt aber auch ein anderer optischer Eindruck eine wichtige Rolle. Betrachten wir einmal Abbildung 1. Der äußere Rahmen soll eine Doppelseite in einem Buch symbolisieren. Die beiden dunkelgrauen Kästen sind die Satzspiegel auf den beiden Seiten. Die hellgrauen Kästen sind Elemente, die in unserem Gehirn unwillkürlich entstehen, obwohl sie auf der Seite normalerweise weiß bleiben. Der Eindruck dieser Kästen entsteht dadurch, dass im Gehirn die Kanten der optischen Ränder des Satzspiegels nach außen verlängert werden. Abhängig von der Größe und Position des Satzspiegels kann dieser Eindruck für einzelne oder alle Kästen stärker oder schwächer sein. Ein besonders harmonischer Eindruck entsteht nun, wenn nicht nur der Satzspiegel dasselbe Seitenverhältnis wie die Seite hat, sondern auch die Kästen A, B und C sowie die quasi liegenden Kästen a, b und c und die ebenfalls liegende Doppelseite. Damit haben praktisch alle optischen Elemente der Seite das gleiche Seitenverhältnis. Ein stärkerer Eindruck von Harmonie ist kaum möglich. Kaum schwächer ist der Eindruck, wenn die Doppelseite und die Kästen a, b und c dasselbe Seitenverhältnis haben, aber dieses Seitenverhältnis vom gemeinsamen Seitenverhältnis der einzelnen Seite, des Satzspiegels und der Kästen A, B und C abweicht. Dies kann wiederum dadurch verstärkt werden, dass die beiden Seitenverhältnisse ihrerseits in einem günstigen Verhältnis zueinander stehen.

Eine interessante Frage ist nun, ob sich die Harmonie besonderer Verhältnisse und die Harmonie der Elemente mit gleichem Seitenverhältnis in Einklang bringen lassen. Ist dies der Fall, dann ist wirklich maximale Harmonie erreicht. Größt mögliche Harmonie lässt gleichzeitig auf eine günstige Satzspiegelkonstruktion schließen. Mindestvoraussetzung der Harmonie ist übrigens - und darüber sind sich alle Typografen einig - die Übereinstimmung des Seitenverhältnisses des Satzspiegels mit dem Seitenverhältnis der Buchseite [3].

Bei der Analyse mittelalterlicher Handschriften erkannte Jan Tschichold übrigens noch eine weitere Harmonie. Er stellte fest, dass bei wertvollen Handschriften der Satzspiegel und - lässt man die kunstvollen Illustrationen weg - der weiße Anteil der Seite ungefähr gleich groß sind. Es ist wenig überraschend, dass Ästheten, Typografen und altgelernte Buchdrucker an einem Großteil der heutigen Büchern vor allem bemängeln, dass die Ränder viel zu schmal und die Satzspiegel viel zu groß sind.

Es gibt noch einen Punkt, über den sich alle Typografen einig sind. Der Fußsteg muss immer größer als der Kopfsteg sein. Der Grund dafür ist einfach: Unser Auge sieht die Mitte des Papiers nicht in der Mitte sondern darüber, jedenfalls dann, wenn darauf eine grau wirkende Fläche liegt. Ähnlich verhält es sich mit dem Bundsteg und dem Außensteg. Wie es scheint ziehen sich die grauen Flächen gegenseitig an. Abbildung 2 zeigt dieselbe Papierfläche und denselben Satzspiegel wie Abbildung 1, allerdings vertikal und horizontal zentriert. In aller Regel werden Sie jedoch den Eindruck haben, dass der Bundsteg breiter ist als der Außensteg und der Kopfsteg breiter als der Fußsteg. Je dunkler die Fläche des Satzspiegels desto stärker wird dieser Eindruck. Ich versichere jedoch, dass der Eindruck täuscht.

Vom Mittelalter bis zur Renaissance
oder „Was können wir von den alten Meistern lernen?“

Im Mittelalter wurden Bücher zwar entweder abgeschrieben oder in Reibetechnik gedruckt, aber Typografie gab es damals schon. Zwar war Typografie im Mittelalter weder Handwerk noch Wissenschaft, aber sie wurde von Schreibern und Druckern gepflegt. Dabei gingen im Idealfall die Fähigkeiten des Meisters auf den Lehrling über und wurden von diesem verbessert. Bekanntlich will die Jugend seit Urzeiten besser als die Alten sein.

Wie bereits im vorigen Kapitel erwähnt, war es im Mittelalter durchaus üblich, dass der Satzspiegel nur ungefähr die Hälfte einer Seite ausmachte. Das wurde dadurch erreicht, dass als Höhe des Satzspiegels oft die Breite des Papiers verwendet wurde. Das verwendete Papier hatte häufig ein Seitenverhältnis von 2 : 3 oder 3 : 4. Die Ränder wurden im Verhältnis Bundsteg : Kopfsteg : Außensteg : Fußsteg von 2 : 3 : 4 : 6 gewählt [4]. Aus Tabelle 2 wissen wir, dass dabei das Verhältnis 2 : 3 des Seitenformats und von Bundsteg : Kopfsteg ebenso im goldenen Schnitt liegt, wie das Verhältnis 1 : 2 von Bundsteg : Außensteg beziehungsweise Kopfsteg : Fußsteg.

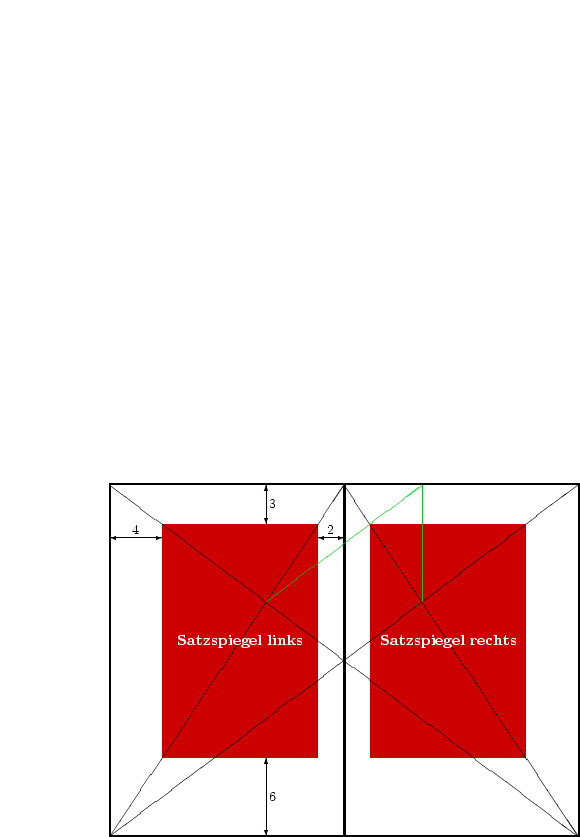
Nehmen wir das Beispiel aus Abbildung 3. Es ergeben sich folgende Verhältnisse:

Die letzten beiden Verhältnisse wurden bei der Konstruktion bewusst so gewählt. Ich komme später darauf zurück. Wie man sieht, genügen drei Verhältnisse, um die Konstruktion vollständig zu beschreiben.

Abbildung 3: Mittelalterliche Satzspiegelkonstruktion mit dem Verhältnis Bundsteg : Kopfsteg : Außensteg : Fußsteg = 2 : 3 : 4 : 6 für Octave-Papier

Die dünnen, schwarzen Linien in der Abbildung sind diagonale Hilfslinien. Unabhängig von der Größe des Satzspiegels muss seine äußere obere Ecke immer auf der Diagonalen der Doppelseite und seine innere obere und äußere untere Ecke immer auf der Diagonalen der Einzelseite liegen. Wenn diese Bedingung erfüllt ist, dann ist auch das Verhältnis 2 : 3 : 4 : 6 sichergestellt. Die beiden dünnen Hilfslinien dienen einer Konstruktion, auf die ich noch zurückkomme.

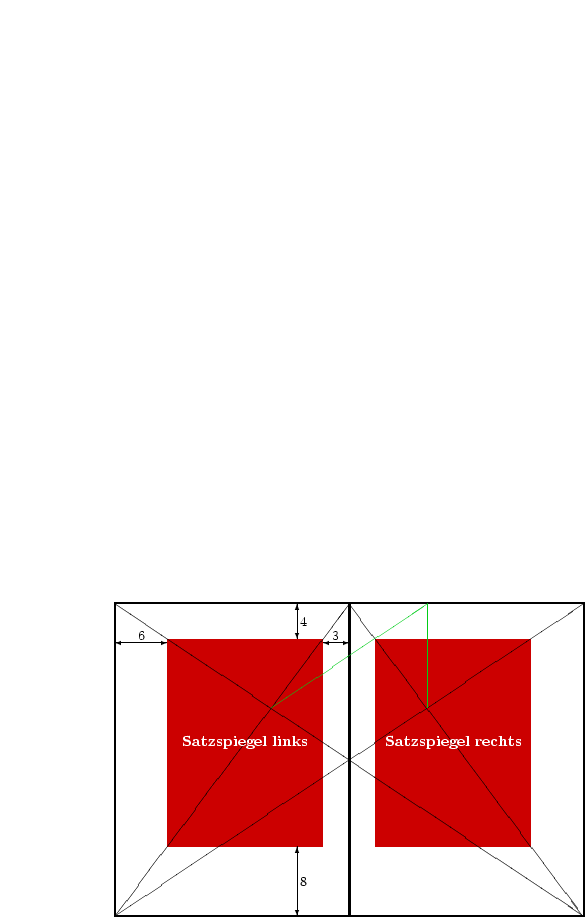
Wie sieht das Ganze nun aus, wenn das Papier nicht das Seitenverhältnis 2 : 3, sondern 3 : 4 hat? Wie bereits erwähnt, erscheint uns dieses Seitenverhältnis ebenfalls harmonisch, auch wenn es im Gegensatz zu 2 : 3 nicht in den goldenen Schnitt passt. Traditionell wird nun das Ränderverhältnis 3 : 4 : 6 : 8 gewählt.

Nehmen wir das Beispiel aus Abbildung 4. Es ergeben sich folgende Verhältnisse:

Abbildung 4: Mittelalterliche Satzspiegelkonstruktion mit dem Verhältnis Bundsteg : Kopfsteg : Außensteg : Fußsteg = 3 : 4 : 6 : 8 für Quart-Papier

In der Renaissance erkannte man den langen, nackten Hals bei Octave offenbar auch. Man versuchte sogleich mit einem einfachen Kunstgriff dieses Problem zu beseitigen, nämlich der Änderung des Ränderverhältnisses von 2 : 3 : 4 : 6 in 2 : 3 : 4 : 5. Abbildung 5 zeigt die Auswirkungen.

Negativ fällt auf, dass das Seitenverhältnis des Satzspiegels nicht mehr mit dem Seitenverhältnis des Papiers übereinstimmt. In der Konstruktion ist das leicht daran zu erkennen, dass das linke untere Eck der linken Seite die Diagonale verlässt. Des Weiteren stehen Bundsteg und Außensteg mit 1 : 2 in einem anderen Verhältnis zueinander als Kopfsteg und Fußsteg mit 3 : 5. Vorteilhaft ist dabei nur, dass beide Verhältnisse dem ganzzahligen goldenen Schnitt entsprechen. Aus dem verletzten Seitenverhältnis resultiert dann natürlich auch, dass die horizontalen Ränder in einem anderen Verhältnis zum Satzspiegel stehen als die vertikalen. Bei idealer Konstruktion wie in den beiden Abbildungen gezeigt, wird dann aus 1 : 2 plötzlich 8 : 19. Dieses Verhältnis passt auch nicht so recht in eines der hamonischen Teilungsverhältnisse. Insgesamt ergibt sich nun ein Wirrwar vieler verschiedener Verhältnisse. Dies ist ein guter Hinweis auf eine gestörte Harmonie.

Einige Typografen lehnen die Renaissance-Konstruktion schon allein wegen des Verstoßes beim Satzspiegelverhältnis ab. Allerdings liegt die Abweichung bei weniger als einem Prozent. Mit Feingefühl kann ein Typograf selbst damit arbeiten. Dem Laien werden jedoch die wenigsten Typografen diese Konstruktion empfehlen, denn in der Praxis können zu dieser konstruktionsbedingten Abweichung weitere Abweichungen kommen.

In der Literatur konnte ich keinen Hinweis darauf finden, dass in der Renaissance diese Abweichung auch auf Quart-Papier übertragen wurde. Ich verzichte hier deshalb ebenfalls darauf, dies zu behandeln. Erwähnt sei jedoch, dass eine ähnliche Abweichung bei Quart beispielsweise durch das Verhältnis 3 : 4 : 6 : 7 erreicht werden könnte.

Die Moderne
oder „Was hat es mit den Hilfslinien auf sich?“

In der Bauhauszeit wurde Ästhetik und die Suche danach zum Prinzip erklärt. Man möge zu dem, was diese Epoche als ästhetisch hervorgebracht hat, stehen wie man will, die Typografie erhielt in dieser Zeit neue und wiederentdeckte Impulse. Für die Satzspiegelkonstruktion von Bedeutung ist, dass zu dieser Zeit die Papiere der DIN-Reihen A, B, C und D bereits Verbreitung gefunden hatten. Es erschien wünschenswert, auf Konstruktionen zurückzugreifen, die unabhängig vom Papierformat funktionieren.

Vermutlich vom holländischen Typografen van de Graaf stammt die Konstruktion, die bereits in den Abbildungen der vorherigen Abschnitte skizziert ist [5]. Man legt dabei zunächst in jede Einzelseite die Diagonale von außen unten nach innen oben. Dann fügt man die Diagonalen der Doppelseite hinzu. Vom Schnittpunkt der ansteigenden Doppelseitendiagonalen mit der Diagonalen der rechten Seite geht man senkrecht nach oben. Von diesem Punkt aus zieht man eine Linie zum Schnittpunkt der abfallenden Doppelseitendiagonalen mit der Diagonalen der linken Seite. Der Schnittpunkt dieser Linie mit der Diagonalen der rechten Seite ist die linke obere Ecke des Satzspiegels der rechten Seite. Die rechte obere Ecke des Satzspiegels ergibt sich dann aus dem Schnittpunkt einer horizontalen Linie von der linken oberen Ecke des Satzspiegels mit der ansteigenden Doppelseitendiagonalen. Der Schnittpunkt einer senkrechten Linie von dieser Ecke mit der Seitendiagonalen bringt dann die rechte untere Ecke. Die vierte Ecke ergibt sich durch die rechten Winkel des Satzpiegels von allein.

Jan Tschichold erkannte, dass diese Konstruktion genau zu der klassischen Einteilung führt, die in den Abbildungen 3 und 4 bereits zu sehen war [7]. Des Weiteren entspricht sie einer Teilung der Papiervertikalen und der Papierhorizontalen in jeweils neun Teile wie sie in Abbildung 6 zu sehen ist.

Doch genug der Verzückung! Einige moderne Typografen bezweifeln, das diese Konstruktion für lebende Kolumnentitel wirklich geeignet ist [5]. Seien wir ehrlich: Der Platz, der für Text nach Abzug der Kolumnentitel bleibt, schwindet dabei. Lebende Kolumnentitel sind darüber hinaus ein Merkmal von wissenschaftlichen Werken, in denen auch häufig Konsutlationselemente wie Tabellen und Abbildungen zu finden sind. Auch für diese wird oft viel Platz in der Höhe und auch in der Breite benötigt. Es ist wenig daher verwunderlich, dass schon Jan Tschichold im letzten Jahrhundert erkannte, dass für technische oder allgemeiner für wissenschaftliche Bücher eine Erweiterung gefunden werden muss. Er fand sie einfach, indem er eine Abweichung von der Verwendung von neun Teilen erlaubte und zum n-mal-n-Raster überging. Daraus resultiert die Rasterkonstruktion.

Bei der Rasterkonstruktion wird die Seite wie bei der Neunerteilung vertikal und horizontal in ein Raster eingeteilt. Dabei werden vertikal und horizontal gleich viele Teile verwendet. Dadurch wird erreicht, dass jedes Kästchen des Rasters dasselbe Seitenverhältnis besitzt wie die Seite. Für den Bundsteg wird eine Spalte, für den Kopfsteg eine Zeile, für den Außensteg zwei Spalten und für den Fußsteg zwei Zeilen des Rasters verwendet. Der Rest ist dann der Satzspiegel. Der einzige Unterschied zur Neunerteilung besteht damit in der Anzahl der Zeilen und Spalten, die verwendet werden. Die Neunerteilung ist also lediglich ein Sonderfall der Rasterkonstruktion.

Die Besonderheit der Rasterkonstruktion besteht darin, dass sie nicht mehr vom Papierformat abhängig ist. Das liegt daran, dass die Verhältnisse Bundsteg : Kopfsteg und Kopfsteg : Außensteg automatisch dem Seitenverhältnis von Satzspiegel und Seite folgen, also die Kästchen A, B, C und a, b, c aus Abbildung 1 automatisch harmonisch sind.

Bedeutet dies nun, dass die Rasterkonstruktion immer ein perfektes Layout liefert? Diese Frage kann mit einem klaren Jain beantwortet werden. Zunächst sollte das Verhältnis Rand : Satzspiegelhöhe beziehungsweise Rand : Satzspiegelbreite in aller Regel nicht größer als 1 : 2 werden. Sonst werden die Ränder eindeutig zu groß. Umgekehrt sollte der kleinste sichtbare Rand nie kleiner als 12,5 mm sein. Dieser Wert erscheint willkürlich und ist es teilweise auch. Dieser Vorwurf trifft allerdings mehr oder weniger für alle Erfahrungswerte zu. Er sollte jedoch nicht als Ausrede dafür dienen, Erfahrungswerte zu ignorieren. Der kleinste sichtbare Rand ist in der Regel der Kopfsteg, da der Bundsteg auf Doppelseiten ja doppelt zu sehen ist. Ein kleinster Rand von 19 mm gilt als nahezu optimal und 25 mm sind elegant. Vermutlich hat letzteres auch irgendwann ein Programmierer gelesen und dann in seine Textverarbeitung als Voreinstellung eingebaut - leider für alle Ränder und leider wurde nie ein Typograf gefragt, ob das so korrekt ist.

Doch die Wahl minimaler oder maximaler Ränder ist nicht das einzige Kriterium. Ebenso wichtig wie ausreichende und nicht übermäßige Randbreiten ist die richtige Breite des Satzspiegels. Hier spielt jedoch der Wert in einem objektiven Maß zunächst eine untergeordnete Rolle. Zwar hat das menschliche Auge klar ein Problem, wenn es vom Ende einer 1 m langen Zeile an deren Anfang zurück soll. So lange man den Kopf beim Lesen aber nicht drehen muss - obwohl man das in der Regel trotzdem macht - ist das Problem der reinen Wegstrecke ein zweitrangiges. Wichtiger ist die Anzahl der Zeichen und die Anzahl der Worte in einer Zeile. Geübte Leser haben bei gut gewählter Schrift mit ordentlichem aber nicht übertriebenem Durchschuss kein Problem beim Verfolgen und Zurückspringen, wenn eine Zeile durchschnittlich nicht mehr als vierundsiebzig Zeichen hat. Angenehm und für ungeübte Leser wünschenswert sind jedoch 62 - 66 Zeichen. Da das Auge in Wirklichkeit nicht von Buchstabe zu Buchstabe, sondern von Wort zu Wort springt, sollten im allgemeinen nicht mehr als 10 - 12 Worte in jeder Zeile stehen. Das begünstigt scheinbar Sprachen mit langen Wörtern oder Wortgefügen. Dem ist nicht so, da das Auge dann wieder nicht mehr von Wort zu Wort, sondern von Teilwort zu Teilwort springt. Dabei spielen Buchstaben mit durchgehenden vertikalen Kanten eine große Rolle. Aber das ist ein anderes Thema.

Das Vorgehen sollte also so sein, dass man zunächst ausmisst, wie breit der Satzspiegel bei der gewählten Schrift maximal sein darf. Dann sucht man nach einem Raster, das zu dieser Breite passt. Als letztes überprüft man ob die Bedingungen bezüglich minimaler und maximaler Ränder eingehalten sind. Wenn die Ränder zu schmal sind, wählt man ein groberes Raster, denn kürzere Zeilen im Satzspiegel sind unproblematisch. Was aber tun, wenn die Ränder zu breit sind? Als Notlösung kann man den Satzspiegel etwas breiter wählen und dafür den Durchschuss erhöhen. Dieses Vorgehen ist aber nur sehr beschränkt anwendbar, etwa bis zu Zeilenlängen von sechsundsiebzig Zeichen und einem Grundlinienabstand von Faktor 1,35 der Schriftgröße. Dabei darf die Schrift auch nicht zu leicht und nicht zu fett sein. Anderenfalls wird der Graueindruck der Seite zu streifig. Die beste Lösung besteht dann darin, entweder das Papierformat oder die Schrift zu wechseln.

Vorteilhaft an der Rasterkonstruktion ist, dass die sehr einfach mit Computerunterstützung umzusetzen ist. Bei KOMA-Script [2] wird genau dies mit dem typearea-Paket erreicht. Bei Verwendung der Option DIVcalc beachtet das Paket ebenfalls Minimalränder. Dabei wird aber als absolutes Minimum nicht die oben erwähnten 12,5 mm, sondern nur 5 mm verwendet.

Seltene Alternativen
oder „Wie kann der goldene Schnitt an Glanz verlieren?“

Wie wir bisher gesehen haben, findet der goldene Schnitt in der einen oder anderen Form in vielen klassischen Satzspiegelkonstruktionen Eingang. Bei der Rasterkonstruktion ist das letztlich nur in Form des Verhältnisses 1 : 2, das quasi die unterste Stufe des ganzzahligen goldenen Schnitts bedeutet und gleichzeitig dem Villardschen Teilungskanon entspricht. Dieses Verhältnis findet sich bei der Rasterkonstruktion wie auch bei den anderen, vorgestellten Konstruktionen als Verhältnis von Bundsteg : Außensteg und eingeschränkt Kopfsteg : Fußsteg. Bei der Neunerteilung findet es sich ebenfalls beim Verhältnis der Anzahl der Zeilen beziehungsweise Spalten, die für den Rand verwendet werden, zu denen die für den Satzspiegel verwendet werden.

Manchmal liest man in der Literatur, dass der goldene Schnitt noch einen Schritt weiter in die Satzspiegelkontruktion Eingang findet. Dann wird als Verhältnis der Ränder 3 : 5 : 8 : 13 verwendet. Dies ist ein Vier-Zahlen-Ausschnitt aus der oben erwähnten Fibonacci-Reihe. Ein erstes Problem dabei ist, dass das Verhältnis von Bundsteg : Außensteg nun nicht mehr 1 : 2, sondern 3 : 8 ist. Das bedeutet, dass der gesamte innere Rand kleiner als jeder äußere Rand ist. Dies ist eine Störung der Harmonie [3]. Immerhin ist dabei der innere Rand 25 Prozent kleiner als jeder Äußere. Dazu kommt, dass das Papier in der Mitte von Büchern häufig gewölbt ist und auch damit optisch eine zusätzliche Verkleinerung des Bundstegs eintreten kann, falls diese bei der Konstruktion nicht kompensiert wird. Ein weiteres Problem besteht darin, dass das Verhältnis Bundsteg : Kopfsteg nicht dem Verhältnis Außensteg : Fußsteg entspricht. Die Kästen A und a aus Abbildung 1 haben also unterschiedliche Seitenverhältnisse. Die Abweichung fällt mit etwa 2,5 Prozent aber tolerierbar gering aus und ist letztlich darin begründet, dass der ganzzahlige goldene Schnitt eben nicht wirklich der goldene Schnitt ist. Dies gilt dann auch für die Möglichkeit, dass der Satzspiegel das Seitenverhältnis der Seite selbst besitzt. Wie inzwischen häufig erwähnt wurde, ist letzteres für die Harmonie sehr wichtig. Stellt sich also die Frage, wann dies beim goldenen Schnitt der Fall ist. Analog zu den Ränderverhältnissen 2 : 3 : 4 : 6 für Octave- und 3 : 4 : 6 : 8 für Quart-Papier sollte beim goldenen Schnitt mit dem Ränderverhältnis 3 : 5 : 8 : 13 das Seitenverhältnis des Papiers dem goldenen Schnitt also 3 : 5 oder 8 : 13 entsprechen. Abbildung 7 zeigt ein Beispiel dafür.

Zusammenfassung
oder „Wie also kann ein Laie einen Satzspiegel beurteilen?“

Nach all den Zahlen schwirrt der Kopf und der Verstand steht still. Daher sei nun noch einmal zusammengefasst, worauf der Laie bei der Beuteilung eines Satzspiegels achten soll. Oberstes Kriterium ist Harmonie.

Grundvorsaussetzung für Harmonie ist, dass das Seitenverhältnis von Satzspiegel und Seite möglichst gut übereinstimmen. Um dies zu überprüfen, zeichnet man eine Diagonale von der oberen inneren zur unteren äußeren Ecke in Seite und Satzspiegel. Sind die Diagonalen parallel, so stimmt das Seitenverhältnis überein.

Günstig ist außerdem, wenn der innere Rand und der äußere Rand gleich groß sind, also der Bundsteg halb so groß wie der Außensteg. Dies ist gegeben, wenn die beiden oben erwähnten Diagonalen direkt aufeinander liegen. Gleichzeitig ist dann der Kopfsteg genau halb so groß wie der Fußsteg und die Kästen A, B, C und a, b, c haben ebenfalls das passende Seitenverhältnis. Überhaupt sollen möglichst wenig unterschiedliche Verhältnisse auftreten. Letztes Kriterium für den Laien ist dann, ob die Zeilenlänge günstig und der Graueindruck einheitlich ist. Geringe Abweichungen bei der Höhe des Satzspiegels und der Höhe des unteren Randes sollte der Laie tolerieren. Ebenso sollte er bei der Kontruktion die Höhe des unteren Randes eher ab- und die Höhe des Satzspiegels eher aufrunden, wenn es darum geht, Nebenbedingungen einzuhalten. Eine Nebenbedingung bei LATEX ist, dass \textheight abzüglich \topskip ein ganzahliges Vielfaches von \baselineskip sein sollte. Dadurch muss bei einer ganz mit einem Absatz gefüllten Seite der Zeilenabstand nicht gedehnt werden.

Der Anwender kann sich das Leben auch erleichtern und das typearea-Paket von KOMA-Script verwenden. Bei Verwendung der Option DIVcalc muss er dort in aller Regel auf gar nichts achten. Bei Vorgabe eines eigenen DIV-Wertes also bei eigener Wahl des Teilungsfaktors für die Rasterkonstruktion muss er lediglich die Zeilenlänge überprüfen, wobei typearea auch hier Unterstützung in Form einer Bewertung des Ergebnisses bietet.

Abschließend sei noch auf ein Zitat aus [6] zurückgegriffen:

Ich hoffe, das notwendige Rüstzeug vermittelt zu haben, damit nun auch Computerbenutzer ihre Bücher weniger willkürlich gestalten und auf Ränder mehr Wert legen.

Glossar
oder „Was versteht man eigentlich unter ...“

In diesem Glossar werden die wichtigsten typografischen Begriffe erklärt, die in diesem Artikel Verwendung finden. Ich habe mir dabei die Freiheit genommen, nicht die Erklärungen aus irgendwelchen Lexika abzuschreiben, sondern meine eigenen Erklärungen und Kommentare abzugeben. Wenn in den Erklärungen ein logischer Ort erwähnt wird, so ist damit ein Ort gemeint, der zum einen mit einem einzigen Begriff bezeichnet werden kann, zum anderen auf linken und rechten Seiten symmetrisch zum Satzspiegel ausgerichtet ist. Beispiele für logische Orte sind: „oben, innen“, „unten, außen“, „mittig, außen“ usw.

Außensteg

Der Außensteg ist der Bereich zwischen der rechten oder linken, äußeren Kante der Seite und dem Satzspiegel. Er wird auch als äußerer Rand bezeichnet.

Bundsteg

Der Bundsteg ist der innere Rand einer Seite. Der Bundsteg der linken Seite bildet mit dem Bundsteg der rechten Seite den inneren Rand. Ob ein Teil des Bundstegs bei der Bindung also durch den Bund verloren geht, oder ob dieser Verlust durch den übergroßen Papierbogen zu kompensieren ist, ist strittig. Unstrittig ist jedoch, dass optische und harmonische Eigenschaften des Bundstegs nur für den sichtbaren Bundsteg angegeben werden können. In diesem Dokument ist daher der Bundsteg mit dem sichtbaren Bundsteg gleichgesetzt.

Fußsteg

Der Fußsteg ist der Bereich zwischen der unteren Kante der Seite und dem Satzspiegel. Er wird auch als unterer Rand bezeichnet.

Kolumnentitel

Man unterscheidet zwischen lebendem und totem Kolumnentitel. Der tote Kolumnentitel ist normalerweise identisch auf jede Seite am gleichen logischen Ort zu finden. Er ist nicht Teil des Satzspiegels. In der Regel ist der tote Kolumnentitel im oberen oder unteren Rand positioniert, wird klein gesetzt und sollte kurz sein. In jedem Fall sollte ein toter Kolumnentitel optisch unauffällig bleiben und so die Harmonie von Satzspiegel und Ränder nicht stören.

Der lebende Kolumnentitel wiederholt Elemente der Gliederung des Dokuments. Er ist Teil des Satzspiegels. In der Regel werden Kapitel- und Abschnittsüberschriften für den lebenden Kolumnentitel verwendet. Er ist auf jeder normalen Textseite am gleichen logischen Ort zu finden. Auf besonderen Seiten, beispielsweise wenn Kolumnentitel und Überschrift mit identischem Text untereinander stehen würden, entfällt der lebende Kolumnentitel. Üblich ist, dass der lebende Kolumnentitel in der ersten Zeile des Satzspiegels positioniert wird.

Kopfsteg

Der Kopfsteg ist der Bereich zwischen der oberen Kante der Seite und dem Satzspiegel. Er wird auch als oberer Rand bezeichnet.

Marginalien

Die Marginalien sind Hinweise, Symbole, Ergänzungen und ähnliche Elemente, die neben dem eigentlichen Text angebracht sind und diesen in der Regel unterstützen. Dünn besetzte Marginalien sind solche, die nur vereinzelt auftreten und optisch nur wenig Platz beanspruchen. Sie befinden sich in der Regel im Außensteg, stelten im Bundsteg. Der Bundsteg wird zum Einen aufgrund seiner Wölbung ausgespart, zum Anderen weil er beim Blättern im Buch nicht ins Auge fällt. Damit können Marginalien im Bundsteg nur eine geringere Wirkung hervorrufen.

Dicht besetzte Marginalien sind solche, die gehäuft auftreten oder optisch sehr viel Platz beanspruchen. Sie würden den optischen Eindruck des Randes und damit die Harmonie der Seite stören. Deshalb sind sie ganz oder teilweise Bestandteil des Satzspiegels.

Octave

Octave ist ein Papierformat mit dem Seitenverhältnis 2 : 3.

Paginierung

Die Paginierung ist die Ausgabe und Positionierung der Seitennummer auf der Seite. Es ist durchaus möglich und statthaft ein Layout zu entwerfen, bei dem auf einer Seite die Seitennummer mehrfach ausgegeben wird. Allerdings sollte die Seitennummer innerhalb eines Dokuments nicht ihren logischen Ort wechseln. Nur so findet der Leser die Seitennummer leicht. Eine Seitennummer, die der Leser nicht leicht findet, ist nutzlos. Die Paginierung ist nicht Teil des Satzspiegels. Es ist jedoch möglich, die Paginierung als Teil des lebenden Kolumnentitels innerhalb des Satzspiegels zu positionieren.

Quart

Quart ist ein Papierformat mit dem Seitenverhältnis 3 : 4.

Satzspiegel

Unter dem Satzspiegel versteht man die gedachte graue Fläche, die sich ergibt, wenn man um den bedruckten Textbereich einen Rahmen zieht. Paginierung, tote Kolumnentitel und dünn besetze Marginalien gehören nicht zum Satzspiegel.

Der Laie denkt oft, dass diese Erklärung den Satzspiegel von den Rändern loslöst, so dass er einen einmal gewählten Satzspiegel frei auf der Seite positioniern kann. Das ist falsch, denn ein Satzspiegel sollte immer Ergebnis einer schematischen Konstruktion sein. Nur so sind wiederholbare und für Laien bewertbare Ergebnisse möglich. Damit ist aber auch die Position des Satzspiegels festgelegt.

Literatur
oder „Wo finde ich mehr zu dem Thema?“